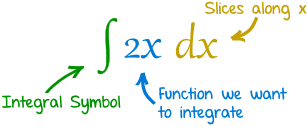Volumes of solids using cross sections and get a 100 on the assessment

Get ready for the assessment on Tuesday!

Things and tips you have to know about finding volumes of solids using cross sections.

For example:  The base of a solid is the region enclosed by the circle x^2 + y^2 =16. Cross-sections
perpendicular to the x-axis are equilateral triangles.

1. Find the key words:

In this given information, cross-sections ... to x-axis and equilateral triangles are key words.

a. Cross- sections.. to x-axis= use dx
    Cross-sections..to y-axis= use dy

b. equilateral triangles= the area formula that needed to be used is 1/2bh

2. Draw out the diagram: It gives you a picture of how does the base of the solid looks like.


（Stole from Mrs. Wahl on google drive)












3. Find out the equation by only contain x in this problem or if it is needed, use substitution on the other problems.

y^2= 16-x^2
-------------------------------------------------------------------------------------------------------------------------

Tips in general:

4. Study the basis formulas for geometry 

5. Proportion of the length for right triangles.
   
        3,4,5 /  1, square root of 3, 2 / 1,2, square root of 5 /5,12,13/ 7,24,25/

6. Do not take the square root sign out of a plus or minus equation.

      For example: y^2= 9-x^2 but we need to find the equation in term of y
                            x^2= 9-y^2
                            x= square root of 9-y^2

        normally we can write it as x= 3-y, but in here we can not !

7. Reading the questions carefully and do not get confused with the information that we do not need at all ! 

For example: the equation of f(x) which is given on the fourth FRQ in practice 3. 

Good luck on Tuesday! 

Review of Assessment

This past week we met three times. Two of the classes we reviewed for our assessment and Friday we took the assessment. Below is a recap of the important things that we should remember for the AP exam.

Volumes of Solids of Revolution

Shapes are all around us. Whether big or small, many are symmetrical and have a volume. With math, and some given functions, we can now find this volume through the techniques of visualization and integration. Finding this volume is the second application of integration as the first was finding area between two curves.

When rotating a line around a specified axis, we will always end up with a shape of which an infinite amount of disks can be sliced. If you are not able to find a direction to slice in order to find these cylinders, you have done something wrong.

If you are incapable of visualizing a certain shape, use this link if you like cheating:
bit.ly/makeasolid 


Slice this way:

Not this way:

As for setting up the graph, always be aware of the axis of rotation. If rotating over the x axis, you will have a dx and integrate in terms of x. Likewise with rotating over the y axis, you will have a dy and variables in terms of y. Being aware of this relationship will make your life much easier.

In cases where you only have one function and will be finding the total volume of the solid, the formula is as simple as:

In this formula, the integrand is the radius squared. This radius is the original function given that was then rotated. There is no second function. The dx means you will integrate with respect to x, slicing down the x axis. The bounds a to b represent either where the function intersects the x axis, given numbers, or where the function may intersect vertical lines given in the problem. The depends entirely on the problem and usually is simple to find. 

Once you have set this formula up, simply integrate normally. I will not go into simple integration in this blog. If needed, check out some of the past few blogs. 

The difficulty to these problems increase slightly when a second function is given. This will usually cut out a chunk of of the solid that would have been created by the outermost function. A second function is also useful to finding the bounds. Sometime these bounds are where the two graphs intersect. Other times vertical or horizontal lines are given which makes finding these bounds easier. Remember that with respect to x, the bounds go left to right on the x axis. When integrating with respect to y, the bounds will go bottom to top on the y axis. 

When given two functions, it is best to make a sketch. Once you have done this, you can clearly see which function is the outer function once rotated. These types of problems will create rings, donuts, washers, or however you want to think of it. This is essential for setting up your integral. 

The formula for finding this volume with two functions is as follows:

In this example, f(x) is the outer function and g(x) is the inner. Essentially this finds the volume of one minus the volume of another, giving you the amount remaining.

After this is set up, the integration is no different. It is often useful to multiply out all the terms before integrating for easier math, but you already knew that.

Remember that when the axis of rotation is not the x or y axis, you will need to account for this. You do so by subtracting the axis from each individual function before you do any squaring or integrating. If the outer function is y - 5 and the axis is x = 3, the function you will use is y - 8. This is logical because you are essentially shifting the function as if x = 3 were the y axis. Don't overcomplicate it.

Here is an example of a two function problem in which there is an outer shell and an inner one. We want the volume between the two.

Find the volume of the solid generated by revolving the region bounded by y = x ² + 2 and y = x + 4 about the x‐axis.

Sketch.

First find where they intersect. These will be the bounds.

Rotate.

                  

Set up and solve.

Integration Applications

This week we began Integral Applications, our fifth and final unit of AP Calculus. Integral Application is used to find the area bound by multiple functions, with respect to either X or Y.

When finding the area bound by two curves with respect to X, use this formula:

Example:

And when finding the area bound by two curves with respect to Y, use this one:

Example:

Tips:

• Always start by graphing the given functions if a graph isn't given.
• When the bounds are not explicitly stated, you can set the functions equal to each other and solve   for the values which will be your bounds.
• When there is no "bottom" function, you must integrate with respect to Y
• When the given functions switch positions, the integrals should be broken up so that the function that is on top acts as f(x).

The Fundamental Theorems of Calculus

The Fundamental Theorem is what we've been working up to all year. It uses derivatives, anti derivatives, and integrals to find the area beneath a graph. It states:
If f is a continuous function on the closed interval [a,b] and F is the anti derivative of f, then:

This means, in cases where we cannot find the integral of the function easily, we can use the anti derivative between two points and end up with the same answer.
The Fundamental theorem leads into the Mean Value theorem for integrals. This is another method which can be used to find the integral of a function. On any graph with the domain [a,b] there are points on the y axis, [f(a),f(b)] There must be a point between them on the graph, called f(c). Using f(c) and the difference between b and a to make a rectangle, we are able to find the integral of the function once again. There is an image of my personal notes, the important part is the graph that shows where f(c) would go.  and  are the two important functions we use from this theorem. f(c) is found by averaging f(a) and f(b).
We also covered the Second Fundamental Theorem of Calculus on Friday. The second theorem involves taking the derivative of a function defined by an integral. The format of the functions change in this theorem:
 the integral is now an equation, and we have two variables. This theorem focuses on the x in the equation. We can use this function to find the derivative of f(x).
The notes below are from class:

They explain how the second theorem is used using a sine equation for an example. We will generally not be concerned about the second variable, as it only changes the line on the graph and not what we are looking to find. The equation wants to find f(2π) so: 

This equation now looks like something we are more used to. The equation is solved like a normal integral, and the answer is 0.
In the second theorem, the first number in the integral, the "a" value, must always be a number. The second one must always be a single variable.
In class, we also found out what to do when the upper bound is not a single x. You need to find the derivative of the function, and use the first theorem to finish solving.

The last thing we looked at was what to do if the bounds of the function were two variables, rather than a number and a variable.

We can use a constant, called a in the notes, to divide the two sides of the bounds. Then, since a constant is needed in the bottom, one of the functions can be flipped, so they both run from a to x. The flipped function only needs to be multiplied by -1 and the two are added back together to find an answer for the specific problem. 

Slope Fields and Solving Differential Equations

Slope Fields - A graphical representation of a differential equation. They are used to visualize the parallel curves that constitute a family of general solutions to a differential equation without actually solving it.

Examples:

dy/dx = x-y/2



Differential Equations
A differential equation contains one or more terms involving derivatives of one variable with respect to another variable.


Example:



This is a general solution to a differential equation.
Another thing you can do is find the particular solution if you are given an initial condition.

Example:

y(2)=-1



-1=1/3(2)^3 + C
C = -11/3
y = 1/3x^2 -11/3

Integration by Substitution

Integration by Substitution is "sort of the reverse Chain Rule".

To integrate using substitution, step one is to choose "u." "u" is a piece of the equation that you want to substitute. Most often, if there is a "ln(x)," choose that to substitute. For example in the equation below, "u" is the part in the parenthesis.

Step 2: Now that we have our "u," we want to take the derivative of it.

u= x²-1
du = 2x*dx

Now that we have du, we want to isolate dx so we can plug it back into the original.

du = 2x*dx
2x = 2x
dx= du
         2x

Step 3: Plug dx into the original function and replace the part of the equation that you used for "u" with "u." 

If you look closely, it appears that the 2x's cancel out and you are left with:

                                                              ∫u4du

Step 4: Now you know how to take the integral of this kind of function and you get:

Step 5: This may look complete, but the "u" is just something we substituted for, so we 

want to replace "u" with what we previously defined it as. 

Completed, the integral would be:

Properties of Integrals

Properties of Integrals:

Different Properties of Integrals can be used to evaluate certain integral equations.

To evaluate an integral:

1. f(x) must be defined

2. The function must be continuous on the interval

Adding/Subtracting Integrals:

 Integrals with an interval of 0:

 Multiplying Integrals by a constant:

 Adding Integrals of adjacent intervals:

 Negative Integrals:

Example from textbook (pg. 290 #2):

a. (-2) ∫f(x)dx = (-2)(-1) = 2

b. ∫f(x)dx + ∫h(x)dx = 5+4 = 9

c. ∫[(2)∫f(x) - (-3)∫h(x)]dx

    (2)∫f(x)dx - (-3)∫h(x)dx = (2)(5)-(-3)(4) = 10+12 = 22

d. ∫f(x)dx = 1

e. (from 1 to 9)∫f(x)dx + (from 7 to 1)∫f(x)dx =  (from 7 to 9)∫f(x)dx =  

    -1 + -∫f(x)dx = 5

    5 +1 = 6

    -6 = (from 1 to 7)∫f(x)dx

f.  ∫h(x)dx - ∫f(x)dx = 4-5 = -1

*keep in mind that the intervals must be the same as what you are evaluating for as I could not type and show that here

Derivatives of Inverse Functions

Inverse Functions:

Inverse functions can be written as f^(-1)(x) and they occur when the y and x values of a function are switched so that the graph flips over dotted line in the example below.



Finding the Derivative of an Inverse Function:

The derivative of an inverse function is the same as the reciprocal of the derivative of the original function when the x value of the inverse function is equal to the y value of the function. In other words, to find the derivative of the function you must:

1. Find the x value of the original function so that the y value original function is equal to the x value of the inverse function.
2. Find the derivative of the original function when x is equal to the x value you found in step 1.
3. Find the derivative of the inverse function by finding the reciprocal of the answer from step 2. (In other words flip the fraction, but remember that the sign does not change)

Example:
Find (f^-1)'(3) when f(x) = -x^2+5

3 = x+5
5-3 = x
2 = x
f'(x) = -2x^1+0 = -2x
f'(2) = -2(2) = -4
(f^-1)'(3) = -1/4

Sometime you are given a chart instead of an equation.

Example:

Find (g^-1)'(3)

3 = g(x)
x = 4
g'(4) = 1/2
(g^-1)'(3) = 2

Intro to Integrals

Riemann Sums

Riemann Sum: a method for approximating area by adding the areas of rectangles.

RRAM- RIGHT Rectangle Approximation Method, using the right endpoint of the graph as the base, and the interval as the height.

LRAM- LEFT Rectangle Approximation Method, using the left endpoint of the graph as the base, and the interval as the height.

MRAM- MIDPOINT Rectangle Approximation Method, using the midpoint of the graph as the base, and the interval as the height. 

TO CALCULATE: interval*(f(x1)+f(x2)+f(x...))

ie. Approximate the area of a region bounded by f(x)=5-x^2 and the x-axis between [0,2]. 

RRAM- .5(f(.5)+f(1)+f(1.5)+f(2))

LRAM- .5(f(0)+f(.5)+f(1)+f(1.5))

MRAM-.5(f(.25)+f(.75)+f(1.25)+f(1.75))

The Trapezoid Rule

Another method of Approximation is the Trapezoid Rule, using trapezoids to find the area under a curve. 

A(trapezoid)= .5h(b1+b2)

Then you just add the areas together. 

A= interval(f(x0) + 2f(x1) + 2(fx2)... + f(xlast))

This is not a Riemann Sum

Integral and Integral Notation

Integral/Integral Notation- The integral is the signed area between the graph of a curve and the x-axis.

How to write an integral goes as pictured above. When typing the integral into a calculator, you must put the domain in which you are finding the integral. If the domain is [a,b], the b goes at the top of the integral symbol, and the a goes on the bottom as prompted by the calculator. It should look like this. 

To enter an integral into your calculator, press the button that is located next to the open book button. Then chose the prompt highlighted below, and type the equation as shown above.