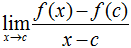1.) The Power Rule
The Power Rule was the most important rule that we learned this week, and this rule explained how to find the derivative of a function instead of using the limit rules. In short, the Power Rule uses the equation for a derivative function to prove that there is an easier and faster way to find the derivative of a function.
 |
| Above is an explanation as to how we got the formula f '(x)=nx^n-1 |
 This is an example of the Power Rule.
This is an example of the Power Rule.
2.) The Constant Multiple Rule
This rule means that if there is a constant in front of the x, then you will multiply the constant by the exponent.
3.) The Sum and Difference Rule
We would use this rule if the function was a polynomial for example, or if it had a constant. This rule states that adding multiple functions together would be the same as adding the derivatives of the same functions together, and the same goes for subtraction.
 This is an example of the Sum and Difference Rule.
This is an example of the Sum and Difference Rule.4.) Derivative of y= sin(x) and y= cos(x)
We use the derivative of sine and cosine graphs to determine what the derivative graphs would look like for some of our trig functions. We found that the derivative graph of sine is cosine and the derivative graph of cosine is negative sine.
 Here are the graphs proving the rule.
Here are the graphs proving the rule. Here are some examples of the rule.
Here are some examples of the rule.5.) The Product Rule
The Product Rule gives us an equation on how to find the derivative when there are two functions multiplied by each other. The equation would be the first function multiplied by the derivative of the second function plus the second function multiplied by the derivative of the first.
 Here is an example of the product rule.
Here is an example of the product rule.6.) The Quotient Rule
The Quotient Rule gives us an equation for finding the derivative of two functions divided by each other.
 Here is an example of the Quotient Rule.
Here is an example of the Quotient Rule.* One great tool to learn to help you memorize the Quotient Rule is:
low, D high; high, D low/low squared
D represents the derivative of and low means the bottom function and high represents the top function.