1. The derivative of a function refers to the slope of a line drawn tangent to a function at a particular point. In order to find the value of the derivative of a function at a particular x-value, you can use the following limit definition:
This definition starts by finding the slope of a secant line between x = a, the point where you want to find the derivative, and some other point on the function. Then, by taking the limit as x approaches a, we are able to consider what happens when the two points become infinitely close together, turning the secant into a tangent.
2. It is also possible to find a formula for the derivative of a function at any point. This is know as the derivative function. The limit definition of the derivative function is:
This is the major definition for the derivative you should know.
3. You can find the equation of a tangent line to a function at a certain x-value if you know the y-value and the derivative of a function as a certain x-value.
For example, if f(2) = 5 and f'(2) = -3, then the equation of the tangent line (in point slope form) is
y - 5 = -3(x - 2)
4. A normal is a line perpendicular to a tangent at a particular point. The process for writing the equation of a normal is the same as writing the equation for a tangent, except that once you find the slope of the tangent, you need to take the negative reciprocal of the tangent slope to find the slope of the normal. So, if f'(2) = -3, then the slope of the normal is 1/3.
5. The slopes of an original function f(x) translate into y-values on the graph of a derivative f'(x).
This means:
- When the graph is increasing, the derivative graph is above the x-axis
- When the graph is decreasing, the derivative graph is below the x-axis
- When the graph has a min, max, or some other kind of horizontal tangent, the derivative graph will have a zero/x-intercept.
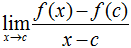

No comments:
Post a Comment