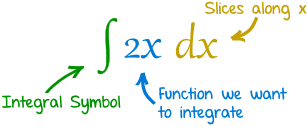Intro to Integrals

Riemann Sums

Riemann Sum: a method for approximating area by adding the areas of rectangles.

RRAM- RIGHT Rectangle Approximation Method, using the right endpoint of the graph as the base, and the interval as the height.

LRAM- LEFT Rectangle Approximation Method, using the left endpoint of the graph as the base, and the interval as the height.

MRAM- MIDPOINT Rectangle Approximation Method, using the midpoint of the graph as the base, and the interval as the height. 

TO CALCULATE: interval*(f(x1)+f(x2)+f(x...))

ie. Approximate the area of a region bounded by f(x)=5-x^2 and the x-axis between [0,2]. 

RRAM- .5(f(.5)+f(1)+f(1.5)+f(2))

LRAM- .5(f(0)+f(.5)+f(1)+f(1.5))

MRAM-.5(f(.25)+f(.75)+f(1.25)+f(1.75))

The Trapezoid Rule

Another method of Approximation is the Trapezoid Rule, using trapezoids to find the area under a curve. 

A(trapezoid)= .5h(b1+b2)

Then you just add the areas together. 

A= interval(f(x0) + 2f(x1) + 2(fx2)... + f(xlast))

This is not a Riemann Sum

Integral and Integral Notation

Integral/Integral Notation- The integral is the signed area between the graph of a curve and the x-axis.

How to write an integral goes as pictured above. When typing the integral into a calculator, you must put the domain in which you are finding the integral. If the domain is [a,b], the b goes at the top of the integral symbol, and the a goes on the bottom as prompted by the calculator. It should look like this. 

To enter an integral into your calculator, press the button that is located next to the open book button. Then chose the prompt highlighted below, and type the equation as shown above.

Concavity and the Second Derivative Test

Concavity and the 2nd Derivative Test

New Vocabulary:

• Inflection Point: 
• Point where the concavity of the graph changes sign.
• Found where f''=0 or undefined
• Concavity
• The curve or shape of a line
• f''>0 the function is concave up (smily face)
• f''<0 the function is concave down (frowny face)

Example:

Determine the open interval on which f(x) is concave up and/or concave down, and all inflection points. f(x)=6 / (x^2+3)

ONE: Find first and second derivative

f(x)=6/(x^2+3)                        **Rearrange function so it is easier to take the first derivative
      =6(x^2+3)^-1

f'(x)= -6 (x^2+3)^-2 (2x)        **Take first derivative and simplify
       = -12x / (x^2+3)^2

f''(x)= [(x^2+3)^2 (-12) - (-12x) (2) (x^2+3) (2x)] / (x^2+3)^4         **Take the derivative
       = (x^2+3) (-12(x^2+3) + 48x^2) / (x^2+3)^4          **Factor out (x^2+3) then cancel with bottom
       = -12 [(x^2+3) - 4x^2] / (x^2 +3)^3                                            ** Factor out -12
       = -12 (-3x^2+3) / (x^2 +3)^3                                                       ** Simply top
       = 36 (x^2-1) / (x^2+3)^3                                          ** Factor out -3 and multiply with -12

TWO: f''(x) = 0 or undefined

f''(x)= 36 (x^2-1) / (x^2+3)^3

36 (x^2-1) = 0                         ** Set top equal to zero to find POSSIBLE inflection points
x= -1, 1                                   ** POSSIBLE Inflection points

Bottom is never undefined! (x^2 +3)^3 can never equal zero

THREE: Plug inflection points into original to find the y-values to the point (use calc.)

f(1) = 6 / (1^2 + 3)^2 = 3/2
f(-1) = 6 / (-1^2 +3)^2 = 3/2

FOUR: Create a number line to test the inflection points

1. Test x= -2, 0, 1 in f''(x) to see if positive or negative (shown below test number)
2. Where f''(x)>0 the function is concave up 
3. Where f''(x)<0 the function is concave down

FIVE: Answer the question

Concave up: (1, infinity) and (- infinity, -1)
Concave down: (-1,1)
Inflection Points: (1, 3/2) and (-1, 3/2)